Heap Sort Algorithm
Heap Sort is a comparison-based sorting algorithm that uses a binary heap data structure (usually a max heap). It repeatedly removes the largest element from the heap and places it at the end of the array.
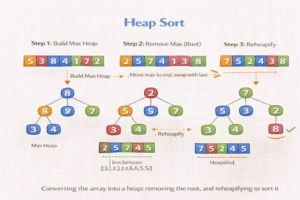
How Heap Sort Works (Step-by-Step)
- Build a Max Heap
- Convert the input array into a max heap.
- In a max heap, the largest element is at the root (index 0).
- Swap Root with Last Element
- Swap the first (largest) element with the last element of the array.
- Reduce Heap Size and Heapify
- Exclude the last element from the heap (it is now in correct position).
- Apply heapify to restore the max heap property.
- Repeat
- Continue the process until the heap size becomes 1.
Example of Heap Sort
Input Array:[5, 3, 8, 4, 1, 7, 2]
Step 1: Build Max Heap
Convert array into max heap:
→ [8, 4, 7, 3, 1, 5, 2]
Step 2: Swap Max (8) with Last (2)
Swap → [2, 4, 7, 3, 1, 5, 8]
Heapify remaining (ignore last sorted element):
→ [7, 4, 5, 3, 1, 2, 8]
Step 3: Swap Max (7) with Last Unsorted (2)
Swap → [2, 4, 5, 3, 1, 7, 8]
Heapify:
→ [5, 4, 2, 3, 1, 7, 8]
Step 4: Swap Max (5) with Last Unsorted (1)
Swap → [1, 4, 2, 3, 5, 7, 8]
Heapify:
→ [4, 3, 2, 1, 5, 7, 8]
Step 5: Swap Max (4) with Last Unsorted (1)
Swap → [1, 3, 2, 4, 5, 7, 8]
Heapify:
→ [3, 1, 2, 4, 5, 7, 8]
Step 6: Swap Max (3) with Last Unsorted (2)
Swap → [2, 1, 3, 4, 5, 7, 8]
Heapify:
→ [2, 1, 3, 4, 5, 7, 8]
Step 7: Swap Remaining
Swap 2 and 1 →
Final Sorted Array →[1, 2, 3, 4, 5, 7, 8]
Heap sort code:
PythonJavaCC++
# Heap Sort
def heapify(arr, n, i):
largest = i
left = 2 * i + 1
right = 2 * i + 2
if left arr[largest]:
largest = left
if right arr[largest]:
largest = right
if largest != i:
arr[i], arr[largest] = arr[largest], arr[i]
heapify(arr, n, largest)
def heap_sort(arr):
n = len(arr)
# Build Max Heap
for i in range(n // 2 - 1, -1, -1):
heapify(arr, n, i)
# Extract elements
for i in range(n - 1, 0, -1):
arr[0], arr[i] = arr[i], arr[0]
heapify(arr, i, 0)
def print_array(arr):
for num in arr:
print(num, end=" ")
print()
arr = [12, 11, 13, 5, 6, 7]
print("Before Sorting:")
print_array(arr)
heap_sort(arr)
print("After Sorting:")
print_array(arr)
public class HeapSort {
// Heap Sort function
public static void heapSort(int[] arr) {
int n = arr.length;
// Build Max Heap
for (int i = n / 2 - 1; i >= 0; i--)
heapify(arr, n, i);
// Extract elements
for (int i = n - 1; i > 0; i--) {
int temp = arr[0];
arr[0] = arr[i];
arr[i] = temp;
heapify(arr, i, 0);
}
}
// Heapify function
public static void heapify(int[] arr, int n, int i) {
int largest = i;
int left = 2 * i + 1;
int right = 2 * i + 2;
if (left arr[largest])
largest = left;
if (right arr[largest])
largest = right;
if (largest != i) {
int swap = arr[i];
arr[i] = arr[largest];
arr[largest] = swap;
heapify(arr, n, largest);
}
}
// Print array
public static void printArray(int[] arr) {
for (int num : arr)
System.out.print(num + " ");
System.out.println();
}
public static void main(String[] args) {
int[] arr = {12, 11, 13, 5, 6, 7};
System.out.println("Before Sorting:");
printArray(arr);
heapSort(arr);
System.out.println("After Sorting:");
printArray(arr);
}
}
#include <stdio.h>
void heapify(int arr[], int n, int i) {
int largest = i;
int left = 2*i + 1;
int right = 2*i + 2;
if (left arr[largest])
largest = left;
if (right arr[largest])
largest = right;
if (largest != i) {
int temp = arr[i];
arr[i] = arr[largest];
arr[largest] = temp;
heapify(arr, n, largest);
}
}
void heapSort(int arr[], int n) {
for (int i = n/2 - 1; i >= 0; i--)
heapify(arr, n, i);
for (int i = n - 1; i > 0; i--) {
int temp = arr[0];
arr[0] = arr[i];
arr[i] = temp;
heapify(arr, i, 0);
}
}
void printArray(int arr[], int n) {
for (int i = 0; i < n; i++)
printf("%d ", arr[i]);
printf("\n");
}
int main() {
int arr[] = {12,11,13,5,6,7};
int n = 6;
printf("Before Sorting:\n");
printArray(arr, n);
heapSort(arr, n);
printf("After Sorting:\n");
printArray(arr, n);
return 0;
}
#include <iostream>
#include <vector>
using namespace std;
void heapify(vector<int>& arr, int n, int i) {
int largest = i;
int left = 2*i + 1;
int right = 2*i + 2;
if (left arr[largest])
largest = left;
if (right arr[largest])
largest = right;
if (largest != i) {
swap(arr[i], arr[largest]);
heapify(arr, n, largest);
}
}
void heapSort(vector<int>& arr) {
int n = arr.size();
for (int i = n/2 - 1; i >= 0; i--)
heapify(arr, n, i);
for (int i = n - 1; i > 0; i--) {
swap(arr[0], arr[i]);
heapify(arr, i, 0);
}
}
void printArray(vector<int> arr) {
for (int num : arr)
cout << num << " ";
cout << endl;
}
int main() {
vector<int> arr = {12,11,13,5,6,7};
cout << "Before Sorting:" << endl;
printArray(arr);
heapSort(arr);
cout << "After Sorting:" << endl;
printArray(arr);
return 0;
}
Time Complexity
| Case | Time Complexity |
| Best Case | O (n log n) |
| Average | O (n log n) |
| Worst Case | O (n log n) |
- Heap sort is not stable.
- It is in-place (no extra space is used except for recursion/heapify).
Space Complexity
- O (1) — It’s an in-place sorting algorithm.
Use Case:
Heap Sort is useful when you need guaranteed O(n log n) performance and don’t mind losing stability.