Graph Representations

To code a graph, we need a way to store these connections in computer memory. The two most common ways are Adjacency Matrix and Adjacency List.

A. Adjacency Matrix

Definition:

An Adjacency Matrix is a 2D array (a grid or table) of size V \times V. If there is a connection between node i and node j, we put a 1 (or the weight) in the cell matrix[i][j]. If there is no connection, we put 0.

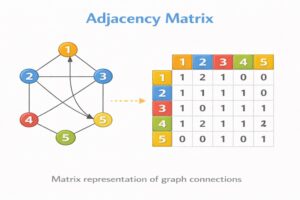
How it Works:

Imagine a spreadsheet where row headers are the source cities and column headers are destination cities. You mark an “X” where a direct flight exists.

Complexity Analysis:

• Space: O(V^2) – Consumes a lot of memory because it stores all possible connections, even if they don’t exist.
• Time (Check connection): O(1) – Very fast lookup.

B. Adjacency List

Definition:

An Adjacency List uses an array (or dictionary) where each index represents a node. Each index stores a list of all the neighbor nodes it connects to.

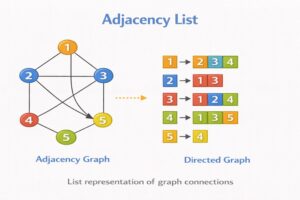
How it Works:

This is like your phone’s contact list. You (Node A) have a list of names you can call. You don’t store a list of everyone in the world with a “No” next to their name; you only list the people you actually know.

Complexity Analysis:

• Space: O(V + E) – Efficient. Only uses memory for actual connections.
• Time (Check connection): O(K) where K is the number of neighbors (degree).

Comparison: Matrix vs. List