Quick Sort Algorithm

Quicksort is an efficient sorting algorithm that follows the divide and conquer strategy. It works by selecting a pivot element and partitioning the array so that all elements smaller than the pivot come before it, and all elements greater come after. This process is repeated for the left and right subarrays until the entire list is sorted.

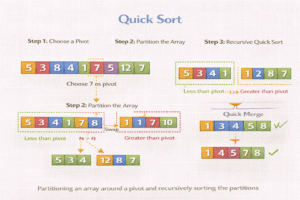
Quick Sort illustration showing pivot selection, partitioning elements into less than and greater than pivot groups, and recursively sorting partitions to form a sorted array.

Working of Quick sort

  1. Pick a Pivot: Choose one number from the list. This is called the pivot.
  2. Divide the List: Rearrange the list so that:
    • All numbers smaller than the pivot go to its left.
    • All numbers greater than the pivot go to its right.
  3. Repeat:
    • Now take the left and right sides (subarrays) and do the same steps again—choose a pivot, divide into smaller and greater parts.
  4. Keep Splitting until each part has only one number.
  5. Once everything is divided like this, the list becomes automatically sorted!

 

Example of Quick Sort 

Given Array:
[5, 3, 8, 4, 1, 12, 7]

Step 1: Choose a Pivot

Take last element as pivot → 7

Rearrange so:

  • Elements < 7 → Left

  • Elements > 7 → Right

After partition:
[5, 3, 4, 1, 7, 8, 12]

Now 7 is in correct position.

Step 2: Apply Quick Sort to Left and Right Parts

Sorting Left Part: [5, 3, 4, 1]

Pivot = 1
Rearranged → [1, 3, 4, 5]

Now sort remaining [3, 4, 5]

Pivot = 5
Rearranged → [3, 4, 5]

Sort [3, 4]
Pivot = 4 → [3, 4]

Left part sorted → [1, 3, 4, 5]

Sorting Right Part: [8, 12]

Pivot = 12
Rearranged → [8, 12]

Right part sorted → [8, 12]

Final Sorted Array

[1, 3, 4, 5, 7, 8, 12]

Quicksort code:

PythonJavaCC++

# Quick Sort

def quick_sort(arr, low, high):

    if low < high:

        pi = partition(arr, low, high)

        quick_sort(arr, low, pi - 1)
        quick_sort(arr, pi + 1, high)


def partition(arr, low, high):

    pivot = arr[high]
    i = low - 1

    for j in range(low, high):

        if arr[j] < pivot:

            i += 1
            arr[i], arr[j] = arr[j], arr[i]

    arr[i + 1], arr[high] = arr[high], arr[i + 1]

    return i + 1


def print_array(arr):

    for num in arr:
        print(num, end=" ")
    print()


arr = [10, 7, 8, 9, 1, 5]

print("Before Sorting:")
print_array(arr)

quick_sort(arr, 0, len(arr) - 1)

print("After Sorting:")
print_array(arr)


public class QuickSort {

    // Quick Sort function
    public static void quickSort(int[] arr, int low, int high) {

        if (low < high) {

            int pi = partition(arr, low, high);

            quickSort(arr, low, pi - 1);
            quickSort(arr, pi + 1, high);
        }
    }

    // Partition function
    public static int partition(int[] arr, int low, int high) {

        int pivot = arr[high];
        int i = low - 1;

        for (int j = low; j < high; j++) {

            if (arr[j] < pivot) {

                i++;

                int temp = arr[i];
                arr[i] = arr[j];
                arr[j] = temp;
            }
        }

        int temp = arr[i + 1];
        arr[i + 1] = arr[high];
        arr[high] = temp;

        return i + 1;
    }

    // Print array
    public static void printArray(int[] arr) {

        for (int num : arr)
            System.out.print(num + " ");

        System.out.println();
    }

    public static void main(String[] args) {

        int[] arr = {10, 7, 8, 9, 1, 5};

        System.out.println("Before Sorting:");
        printArray(arr);

        quickSort(arr, 0, arr.length - 1);

        System.out.println("After Sorting:");
        printArray(arr);
    }
}


#include <stdio.h>

int partition(int arr[], int low, int high) {

    int pivot = arr[high];
    int i = low - 1;

    for (int j = low; j < high; j++) {

        if (arr[j] < pivot) {

            i++;

            int temp = arr[i];
            arr[i] = arr[j];
            arr[j] = temp;
        }
    }

    int temp = arr[i + 1];
    arr[i + 1] = arr[high];
    arr[high] = temp;

    return i + 1;
}

void quickSort(int arr[], int low, int high) {

    if (low < high) {

        int pi = partition(arr, low, high);

        quickSort(arr, low, pi - 1);
        quickSort(arr, pi + 1, high);
    }
}

void printArray(int arr[], int n) {

    for (int i = 0; i < n; i++)
        printf("%d ", arr[i]);

    printf("\n");
}

int main() {

    int arr[] = {10,7,8,9,1,5};
    int n = 6;

    printf("Before Sorting:\n");
    printArray(arr, n);

    quickSort(arr, 0, n - 1);

    printf("After Sorting:\n");
    printArray(arr, n);

    return 0;
}


#include <iostream>
#include <vector>
using namespace std;

int partition(vector<int>& arr, int low, int high) {

    int pivot = arr[high];
    int i = low - 1;

    for (int j = low; j < high; j++) {

        if (arr[j] < pivot) {

            i++;
            swap(arr[i], arr[j]);
        }
    }

    swap(arr[i + 1], arr[high]);

    return i + 1;
}

void quickSort(vector<int>& arr, int low, int high) {

    if (low < high) {

        int pi = partition(arr, low, high);

        quickSort(arr, low, pi - 1);
        quickSort(arr, pi + 1, high);
    }
}

void printArray(vector<int> arr) {

    for (int num : arr)
        cout << num << " ";

    cout << endl;
}

int main() {

    vector<int> arr = {10,7,8,9,1,5};

    cout << "Before Sorting:" << endl;
    printArray(arr);

    quickSort(arr, 0, arr.size() - 1);

    cout << "After Sorting:" << endl;
    printArray(arr);

    return 0;
}

Time Complexity

Case Time Complexity Explanation
Best Case O (n log n) When the pivot always splits the array into two equal halves.
Average Case O (n log n) On average, Quicksort performs well with balanced partitions.
Worst Case O(n²) Happens when the pivot is always the smallest or largest element (e.g., sorted array with bad pivot choice).
     
PreviousNext