Insertion Sort Algorithm
Insertion sort is a sorting algorithm that places an unsorted element at its suitable place in each iteration.
Insertion sort works similarly as we sort cards in our hand in a card game.
We assume that the first card is already sorted then, we select an unsorted card. If the unsorted card is greater than the card in hand, it is placed on the right otherwise, to the left. In the same way, other unsorted cards are taken and put in their right place.
A similar approach is used by insertion sort.
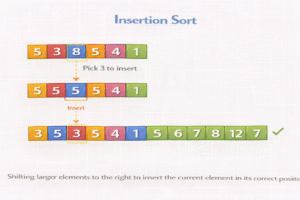
Working of Insertion Sort
Insertion Sort builds the sorted array one element at a time, by comparing each new element with the already sorted part and inserting it in the correct position.
Step-by-Step Working:
- Start from the second element, assuming the first element is already sorted.
- Compare the current element with the elements in the sorted part (to its left).
- Shift all larger elements in the sorted part one position to the right.
- Insert the current element into its correct position in the sorted part.
- Repeat steps 2 to 4 for all remaining elements in the array.
- After the last pass, the entire array will be sorted.
Example of Insertion Sort
Given Array:[5, 3, 8, 4, 1, 12, 7]
Pass 1:
Key = 3
Compare with 5 → 3 < 5 → Shift 5
Insert 3
Result: [3, 5, 8, 4, 1, 12, 7]
Pass 2:
Key = 8
Compare with 5 → 8 > 5 → No shift
Insert at same place
Result: [3, 5, 8, 4, 1, 12, 7]
Pass 3:
Key = 4
Compare with 8 → Shift 8
Compare with 5 → Shift 5
Compare with 3 → Stop
Insert 4
Result: [3, 4, 5, 8, 1, 12, 7]
Pass 4:
Key = 1
Compare with 8, 5, 4, 3 → Shift all
Insert at beginning
Result: [1, 3, 4, 5, 8, 12, 7]
Pass 5:
Key = 12
Compare with 8 → No shift
Insert at same place
Result: [1, 3, 4, 5, 8, 12, 7]
Pass 6:
Key = 7
Compare with 12 → Shift 12
Compare with 8 → Shift 8
Compare with 5 → Stop
Insert 7
Result: [1, 3, 4, 5, 7, 8, 12]
Final Sorted Array:
[1, 3, 4, 5, 7, 8, 12]
Insertion sort Java code:
public class InsertionSort {
// Function to perform Insertion Sort
public static void insertionSort(int[] arr) {
int n = arr.length;
// Start from second element (index 1)
for (int i = 1; i < n; i++) { int key = arr[i]; // Element to be inserted int j = i - 1; // Move elements greater than key one position ahead while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j--;
}
// Insert key at correct position
arr[j + 1] = key;
}
}
// Function to print array
public static void printArray(int[] arr) {
for (int num : arr) {
System.out.print(num + " ");
}
System.out.println();
}
// Main method
public static void main(String[] args) {
int[] arr = {12, 11, 13, 5, 6};
System.out.println("Before Sorting:");
printArray(arr);
insertionSort(arr);
System.out.println("After Sorting:");
printArray(arr);
}
}
Time Complexity of Insertion Sort:
| Case | Time Complexity | Explanation |
| Best Case | O(n) | When the array is already sorted. Only n-1 comparisons, no shifting needed. |
| Average Case | O(n²) | Random order elements; shifting needed in about half of the comparisons. |
| Worst Case | O(n²) | When the array is in reverse order; each element must be compared and shifted. |
Space Complexity:
- O (1) (in-place sorting, uses no extra space)
Note:
Insertion Sort is efficient for small or nearly sorted datasets and is adaptive, unlike Selection Sort. It is also stable, meaning it maintains the relative order of equal elements.