Queue

Queue is an abstract data structure, somewhat similar to Stacks. Unlike stacks, a queue is open at both its ends. One end is always used to insert data (enqueue) and the other is used to remove data (dequeue). Queue follows First-In-First-Out methodology, i.e., the data item stored first will be accessed first.

Reference Video: Queue

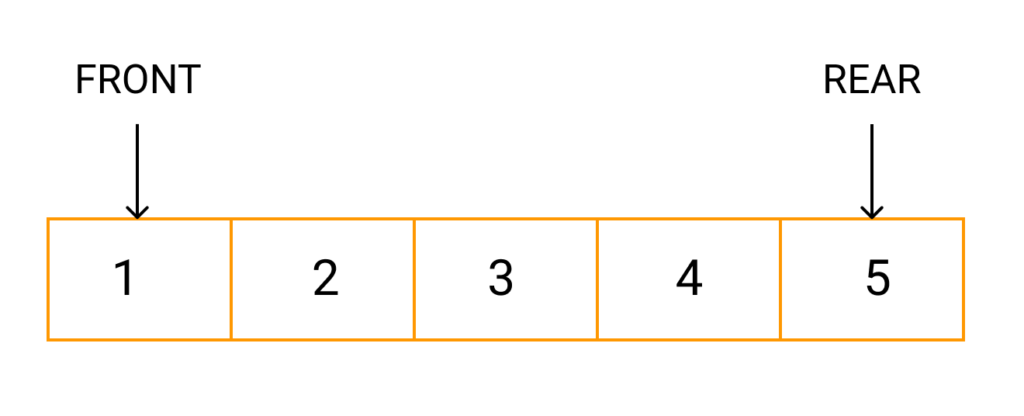
Queue Representation

As we now understand that in queue, we access both ends for different reasons. The following diagram given below tries to explain queue representation as data structure −

Basic Operations

Queue operations may involve initializing or defining the queue, utilizing it, and then completely erasing it from the memory. Here we shall try to understand the basic operations associated with queues −

• enqueue() − add (store) an item to the queue.
• dequeue() − remove (access) an item from the queue.

Few more functions are required to make the above-mentioned queue operation efficient. These are −

• peek() − Gets the element at the front of the queue without removing it.
• isfull() − Checks if the queue is full.
• isempty() − Checks if the queue is empty.

In queue, we always dequeue (or access) data, pointed by front pointer and while enqueing (or storing) data in the queue we take help of rear pointer.

• peek() – This function helps to see the data at the front of the queue. The algorithm of peek() function is as follows −

Algorithm:

begin procedure peek return queue[front]

end procedure

isfull()

As we are using single dimension array to implement queue, we just check for the rear pointer to reach at MAXSIZE to determine that the queue is full. In case we maintain the queue in a circular linked-list, the algorithm will differ. Algorithm of isfull() function

Algorithm

begin procedure isfull

if rear equals to MAXSIZE return true

else

return false endif

end procedure

isempty()

Algorithm of isempty() function −

Algorithm:

begin procedure isempty

if front is less than MIN OR front is greater than rear return true

else

return false endif

end procedure

If the value of front is less than MIN or 0, it tells that the queue is not yet initialized, hence empty.

Enqueue Operation

Queues maintain two data pointers, front and rear. Therefore, its operations are comparatively difficult to implement than that of stacks.

The following steps should be taken to enqueue (insert) data into a queue −

• Step 1 − Check if the queue is full.
• Step 2 − If the queue is full, produce overflow error and exit.
• Step 3 − If the queue is not full, increment rear pointer to point the next empty space.
• Step 4 − Add data element to the queue location, where the rear is pointing.
• Step 5 − return success.

Sometimes, we also check to see if a queue is initialized or not, to handle any unforeseen situations.

Algorithm for enqueue operation

procedure enqueue(data) if queue is full return overflow

endif

rear ← rear + 1 queue[rear] ← data

return true

end procedure

Dequeue Operation

Accessing data from the queue is a process of two tasks − access  the data where front is pointing and remove the data after access. The following steps are taken to perform dequeue operation −

• Step 1 − Check if the queue is empty.
• Step 2 − If the queue is empty, produce underflow error and exit.
• Step 3 − If the queue is not empty, access the data where front is pointing.
• Step 4 − Increment front pointer to point to the next available data element.
• Step 5 − Return success.

Algorithm for dequeue operation

procedure dequeue

if queue is empty return underflow

end if

data = queue[front] front ← front + 1 return true

end procedure

Evaluation of Expression

The way to write arithmetic expression is known as a notation. An arithmetic expression can be written in three different but equivalent notations, i.e., without changing the essence or output of an expression. These notations are –

• Infix Notation
• Prefix (Polish) Notation
• Postfix (Reverse-Polish) Notation

These notations are named as how they use operator in expression. We shall learn the same here in this chapter.

Infix Notation

We write expression in infix notation, e.g. a – b + c, where operators are used in– between operands. It is easy for us humans to read, write, and speak in infix notation but the same does not go well with computing devices. An algorithm to

process infix notation could be difficult and costly in terms of time and space consumption.

Prefix Notation

In this notation, operator is prefixed to operands, i.e. operator is written ahead of operands. For example, +ab. This is equivalent to its infix notation a + b. Prefix notation is also known as Polish Notation.

Postfix Notation

This notation style is known as Reversed Polish Notation. In this notation style, the operator is postfixed to the operands i.e., the operator is written after the operands. For example, ab+. This is equivalent to its infix notation a + b.

The following table briefly tries to show the difference in all three notations −

Sr.No.	Infix Notation	Prefix Notation	Postfix Notation
1	a + b	+ a b	a b +
2	(a + b) ∗ c	∗ + a b c	a b + c ∗
3	a ∗ (b + c)	∗ a + b c	a b c + ∗
4	a / b + c / d	+ / a b / c d	a b / c d / +
5	(a + b) ∗ (c + d)	∗ + a b + c d	a b + c d + ∗
6	((a + b) ∗ c) – d	– ∗ + a b c d	a b + c ∗ d –

Parsing Expressions

As we have discussed, it is not a very efficient way to design an algorithm or program to parse infix notations. Instead, these infix notations are first converted into either postfix or prefix notations and then computed.

To parse any arithmetic expression, we need to take care of operator precedence and associativity also.

Precedence

When an operand is in between two different operators, which operator will take the operand first, is decided by the precedence of an operator over others. For example –

a+b*c -🡪 a+(b*c)

As multiplication operation has precedence over addition, b * c will be evaluated first. A table of operator precedence is provided later.

Associativity

Associativity describes the rule where operators with the same precedence appear in an expression. For example, in expression a + b − c, both + and – have the same precedence, then which part of the expression will be evaluated first, is determined by associativity of those operators. Here, both + and − are left associative, so the expression will be evaluated as (a + b) − c.

Precedence and associativity determines the order of evaluation of an expression. Following is an operator precedence and associativity table (highest to lowest) −

Sr.No.	Operator	Precedence	Associativity
1	Exponentiation ^	Highest	Right Associative
2	Multiplication ( ∗ ) & Division ( / )	Second Highest	Left Associative
3	Addition ( + ) & Subtraction ( − )	Lowest	Left Associative

The above table shows the default behavior of operators. At any point of time in expression evaluation, the order can be altered by using parenthesis. For example:

In a + b*c, the expression part b*c will be evaluated first, with multiplication as precedence over addition. We here use parenthesis for a + b to be evaluated first, like (a + b)*c.

Postfix Evaluation Algorithm

Step 1 − scan the expression from left to right Step 2 − if it is an operand push it to stack

Step 3 − if it is an operator pull operand from stack and perform operation

Step 4 − store the output of step 3, back to stack

Step 5 − scan the expression until all operands are consumed Step 6 − pop the stack and perform operation

A postfix expression is a collection of operators and operands in which the operator is placed after the operands. That means, in a postfix expression the operator follows the operands.

Postfix Expression has following general structure…