Heap Sort Algorithm

Heap Sort is a comparison-based sorting algorithm that uses a binary heap data structure (usually a max heap). It repeatedly removes the largest element from the heap and places it at the end of the array.

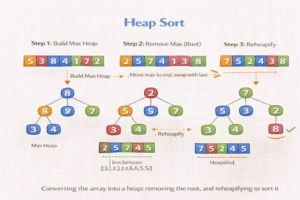
 How Heap Sort Works (Step-by-Step)

1. Build a Max Heap

• Convert the input array into a max heap.
• In a max heap, the largest element is at the root (index 0).

2. Swap Root with Last Element

• Swap the first (largest) element with the last element of the array.

3. Reduce Heap Size and Heapify

• Exclude the last element from the heap (it is now in correct position).
• Apply heapify to restore the max heap property.

4. Repeat

• Continue the process until the heap size becomes 1.

Example

Input Array: [4, 10, 3, 5, 1]

Step 1: Build Max Heap

→ [10, 5, 3, 4, 1]

Step 2: Swap max (10) with last (1)

→ [1, 5, 3, 4, 10]
→ Heapify → [5, 4, 3, 1, 10]

Step 3: Swap max (5) with 4th (1)

→ [1, 4, 3, 5, 10]
→ Heapify → [4, 1, 3, 5, 10]

Step 4: Swap max (4) with 3rd (3)

→ [3, 1, 4, 5, 10]
→ Heapify → [3, 1, 4, 5, 10]

Step 5: Swap 3 and 1

→ [1, 3, 4, 5, 10] Sorted!

Heap sort Python code:

function heapSort(arr):

    buildMaxHeap(arr)

    for i = len(arr)-1 to 1:

        swap(arr [0], arr[i])

        heapify(arr, 0, i)

function heapify(arr, i, n):

    largest = i

    left = 2 * i + 1

    right = 2 * i + 2

    if left < n and arr[left] > arr[largest]:

        largest = left

    if right < n and arr[right] > arr[largest]:

        largest = right

    if largest != i:

        swap(arr[i], arr[largest])

        heapify(arr, largest, n)

Time Complexity

• Heap sort is not stable.
• It is in-place (no extra space is used except for recursion/heapify).

 Space Complexity

• O (1) — It’s an in-place sorting algorithm.

Use Case:

Heap Sort is useful when you need guaranteed O(n log n) performance and don’t mind losing stability.